|
Download Excel spreadsheet (ZIP file, 12KB) This Excel spreadsheet is intended as a teaching aid. It shows the waveforms created by adding various combinations of harmonics with various phase relationships.
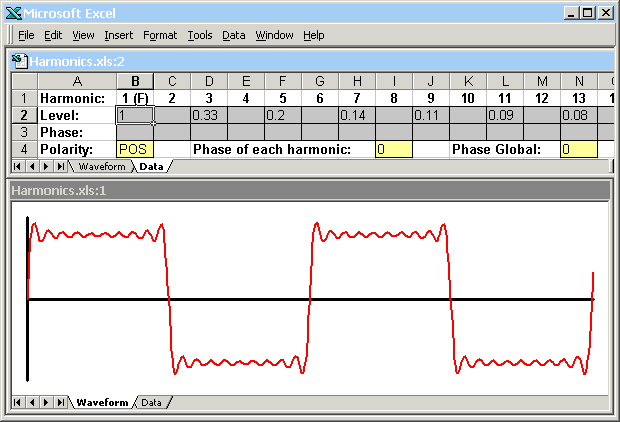
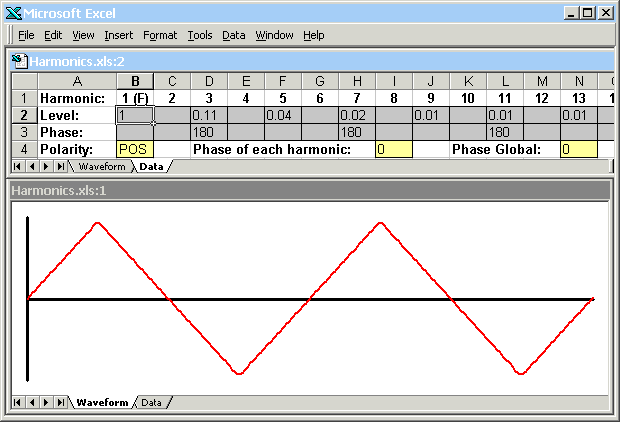
The spreadsheet has two windows: one into which the level and phase of each harmonic is entered, and one that shows the resulting waveform. The waveform always shows two complete cycles (periods) and is scaled to fit the height of the window. As a result of this scaling, the absolute values of the numbers entered for the levels of the harmonic components are unimportant; it is only the ratio between harmonics that matters. The level of each harmonic is entered into row two of the spreadsheet, and the phase of each harmonic (in degrees) is entered into row three. Row four of the spreadsheet allows the polarity of the waveform to be inverted (set to "POS" or "NEG"), for a given phase shift (in degrees) to be added to every harmonic, or for the phase of the complete waveform to be shifted (by adding a phase shift to each harmonic proportional to the harmonic number). It also allows a DC offset to be added. The spreadsheet handles the first twenty harmonics only. For frequencies above around 1kHz, therefore, it gives an approximation of what the ear hears (because the twentieth harmonic of 1kHz is 20kHz which is outside of the range of human hearing). Further down the spreadsheet are sets of harmonic and phase data for sawtooth waves, square waves, and triangle waves. These waveforms may be displayed by copying data from the appropriate rows and pasting it over rows 2 and 3. The illustrations show the resulting square wave (above) and triangle wave (below) displays.
A sawtooth wave contains every harmonic, and the amount of harmonic number n is given by 1/n. A square wave has the same harmonic proportions as the sawtooth wave but contains only odd harmonics. A triangle wave also contains only odd harmonics, but the amount of harmonic number n is given by 1/(n^2). In addition, for the wave to look triangular, the phase of every other harmonic present (numbers 3, 7, 11, 15, and so on) must be shifted by 180 degrees. © 2014, 100dB sound |